hypothesis two categorical variables

• Conferences
• Last updated May 17, 2022
• In AI Mysteries

How to use the Chi-Square Test for two categorical variables?

Illustration by Analytics India Magazine

• Published on May 17, 2022
• by Sourabh Mehta

The Chi-Square test of independence examines whether or not two nominal (categorical) variables have a significant connection. Comparing the frequency of categories for one nominal variable with the frequency of categories for the second nominal variable. There are two utilizations of the chi-square test to check the independence of variables and to check the goodness of fit . In the article, we will be discussing the when and where the chi-square test could be utilized. Following are the topics to be covered.

Table of contents

A brief about chi-square.

• Uses of chi-square

Implementing chi-square test

Let’s start by talking about the chi-square test.

The objective is to determine whether the association between two qualitative variables is statistically significant. 

The formulation of the hypotheses for this statistical analysis is something like this.

• Null Hypothesis (H0): There is no substantial relationship between the two variables (in case of independence test), or there is no difference in variable distribution (in case of goodness of fit). 
• Alternative Hypothesis (H1): There is a substantial relationship between variables (in case of independence test) or a significant variation in variable distribution (in case of goodness of fit).

When the null hypothesis is true, the anticipated values for each cell in the table must be specified. The anticipated values describe what the values of each cell in the table would be if the two variables were not associated. The sample size, row totals, and column totals are all required by the algorithm for calculating anticipated values.

The chi-square statistic compares observed and anticipated values. This test statistic is used to see if the discrepancy between observed and predicted values is statistically significant.

Are you looking for a complete repository of Python libraries used in data science,  check out here .

Uses of Chi-square test

A chi-square test is used to examine if observed findings are consistent with predicted outcomes and to rule out the possibility that observations are due to chance. When the data being studied is from a random sample and the variable in issue is a categorical variable, the chi-square test is applicable. These sorts of data are frequently gathered through survey replies or questionnaires. As a result, chi-square analysis is frequently the most effective in assessing this sort of data.

There are two main kinds of chi-square tests: the test of independence and the goodness-of-fit test.

Independence

When considering categorical variables that may be interdependent. A chi-square test for independence might be used to assess the association between categorical variables.

Assume there are two variables: gender and degree course and need to check whether gender depends on the course or course depends on gender. Then, using the chi-square formula of observed and predicted values, compare the frequency with which male and female employees choose from the available courses.

If there is no relationship between gender and course, implying that they are independent of one another, then the actual frequencies at which both genders choose each offered course should be expected to be approximately equal. The ratio of the gender of students in any selected degree should be approximately equal to the ratio of the gender in the sample.

A chi-square test for independence might indicate how probable it is that any observed divergence between the actual frequencies in the data and these theoretical predictions can be explained by random chance.

Goodness-of-Fit

The chi-square provides a way to test how well a sample of data matches the characteristics of the larger population that the sample is intended to represent. The sample data cannot be used to draw conclusions about the larger population if they do not reflect those of the target population. This kind of chi-square test is goodness-of-fit.

Assume a small library has the greatest number of members on Fridays and Sundays the average amount on Mondays, Tuesdays, and Saturdays, and the fewest on Wednesdays and Thursdays. Based on these predictions, the library hires a set number of employees each day to check in members, clean facilities, guards, and librarians.

However, the library is losing money, and the owner wants to determine if the frequency of member assumptions and staffing levels are right. For six weeks, the owner chooses to count the number of library visitors every day. They can then use a chi-square goodness-of-fit test to compare the library’s assumed attendance to its observed attendance. With the additional information, they can better manage the library and increase revenue.

Let’s implement this test on a dataset and solve some problems using python

In python, the scipy library offers a stats module under which we can find all the chi-square test-related attributes.

Let’s check the independence of categorical variables

To check the dependency of interested categorical variables need to create a contingency table because the chi-square test could only be performed at tables.

Checking the dependency between the education level of employees and their graduation degree.  So the contingency table is made for them and it looks like the above image.

Now this table is an input in the chi-square function offered by spicy. This function will calculate the test statistics value, p-value, degrees of freedom and expected values.

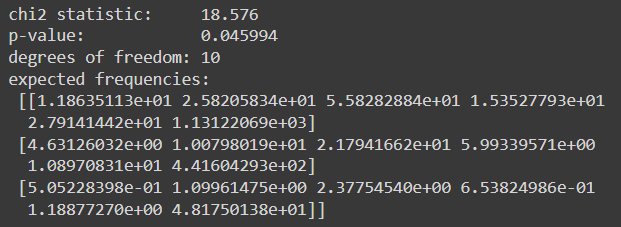
The critical value for the chi-square test with a degree of freedom of 10 and alpha 0.05 is 18.307. Since the test statistic (18.576) exceeds the critical value the null hypothesis is rejected. Therefore, the education level and the graduation degree are dependent on each other.

Let’s check the goodness-of-fit of gender and relevant experience. In this test, the chi-square will fit one categorical variable to a distribution. The process is the same as the above: create a contingency table and use the formula but in this let’s do it from scratch rather than directly applying the contingency chi-square function. 

Now calculate the observed and expected values and degrees of freedom

We are all set to calculate the chi-square static value

The critical value for the chi-square test with a degree of freedom of 2 and alpha 0.05 is 5.991. Since the test statistic (10.861) exceeds the critical value the null hypothesis is rejected. Therefore, gender and relevant experience have a significant variation in the distribution. This could be concluded that there is a substantial dependency of gender on relevant experience according to the data.

Chi-square is the test for understanding the relationship between two categorical variables. One can understand whether the dependency and fitness of categorical variables are related to others. With this hands-on implementation, we understood the chi-square test and when to use chi-square. 

• Link to the above codes
• Read further about chi-square

📣 Want to advertise in AIM? Book here

Sourabh Mehta

Popular Categories :

AI News | Course & Certifications  | Top AI Tools

Since both ITs and GCCs are competing for the same talent pool, with the GCCs offering significantly higher packages and better designations to freshers, it gets challenging for IT.

Top Editorial Picks

Dear Investors, Our Failure is on You: Startup Founders Vandana Nair

Meet the Indian AI Startup Quietly Taking Over the Enterprise World Siddharth Jindal

How AI Dragons Set GenAI on Fire This Year Tarunya S

Karnataka Brings GCC Policy, Aims to Create 3.5 Lakh Jobs by 2029 Sanjana Gupta

2024 Marks the End of Moore’s Law Tarunya S

No Noise, Only Sound – How AI is Changing Our Hearing Aids Vidyashree Srinivas

Subscribe to The Belamy: Our Weekly Newsletter

Biggest ai stories, delivered to your inbox every week..

© Analytics India Magazine Pvt Ltd & AIM Media House LLC 2024

• Terms of use
• Privacy Policy

India's Biggest Developers Summit

5-7th feb 2025, bangalore.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

10.1 - setting the hypotheses: examples.

A significance test examines whether the null hypothesis provides a plausible explanation of the data. The null hypothesis itself does not involve the data. It is a statement about a parameter (a numerical characteristic of the population). These population values might be proportions or means or differences between means or proportions or correlations or odds ratios or any other numerical summary of the population. The alternative hypothesis is typically the research hypothesis of interest. Here are some examples.

Example 10.2: Hypotheses with One Sample of One Categorical Variable Section  

About 10% of the human population is left-handed. Suppose a researcher at Penn State speculates that students in the College of Arts and Architecture are more likely to be left-handed than people found in the general population. We only have one sample since we will be comparing a population proportion based on a sample value to a known population value.

• Research Question : Are artists more likely to be left-handed than people found in the general population?
• Response Variable : Classification of the student as either right-handed or left-handed

State Null and Alternative Hypotheses

• Null Hypothesis : Students in the College of Arts and Architecture are no more likely to be left-handed than people in the general population (population percent of left-handed students in the College of Art and Architecture = 10% or p = .10).
• Alternative Hypothesis : Students in the College of Arts and Architecture are more likely to be left-handed than people in the general population (population percent of left-handed students in the College of Arts and Architecture > 10% or p > .10). This is a one-sided alternative hypothesis.

Example 10.3: Hypotheses with One Sample of One Measurement Variable Section  

A generic brand of the anti-histamine Diphenhydramine markets a capsule with a 50 milligram dose. The manufacturer is worried that the machine that fills the capsules has come out of calibration and is no longer creating capsules with the appropriate dosage.

• Research Question : Does the data suggest that the population mean dosage of this brand is different than 50 mg?
• Response Variable : dosage of the active ingredient found by a chemical assay.
• Null Hypothesis : On the average, the dosage sold under this brand is 50 mg (population mean dosage = 50 mg).
• Alternative Hypothesis : On the average, the dosage sold under this brand is not 50 mg (population mean dosage ≠ 50 mg). This is a two-sided alternative hypothesis.

Example 10.4: Hypotheses with Two Samples of One Categorical Variable Section  

Many people are starting to prefer vegetarian meals on a regular basis. Specifically, a researcher believes that females are more likely than males to eat vegetarian meals on a regular basis.

• Research Question : Does the data suggest that females are more likely than males to eat vegetarian meals on a regular basis?
• Response Variable : Classification of whether or not a person eats vegetarian meals on a regular basis
• Explanatory (Grouping) Variable: Sex
• Null Hypothesis : There is no sex effect regarding those who eat vegetarian meals on a regular basis (population percent of females who eat vegetarian meals on a regular basis = population percent of males who eat vegetarian meals on a regular basis or p females = p males ).
• Alternative Hypothesis : Females are more likely than males to eat vegetarian meals on a regular basis (population percent of females who eat vegetarian meals on a regular basis > population percent of males who eat vegetarian meals on a regular basis or p females > p males ). This is a one-sided alternative hypothesis.

Example 10.5: Hypotheses with Two Samples of One Measurement Variable Section  

Obesity is a major health problem today. Research is starting to show that people may be able to lose more weight on a low carbohydrate diet than on a low fat diet.

• Research Question : Does the data suggest that, on the average, people are able to lose more weight on a low carbohydrate diet than on a low fat diet?
• Response Variable : Weight loss (pounds)
• Explanatory (Grouping) Variable : Type of diet
• Null Hypothesis : There is no difference in the mean amount of weight loss when comparing a low carbohydrate diet with a low fat diet (population mean weight loss on a low carbohydrate diet = population mean weight loss on a low fat diet).
• Alternative Hypothesis : The mean weight loss should be greater for those on a low carbohydrate diet when compared with those on a low fat diet (population mean weight loss on a low carbohydrate diet > population mean weight loss on a low fat diet). This is a one-sided alternative hypothesis.

Example 10.6: Hypotheses about the relationship between Two Categorical Variables Section  

• Research Question : Do the odds of having a stroke increase if you inhale second hand smoke ? A case-control study of non-smoking stroke patients and controls of the same age and occupation are asked if someone in their household smokes.
• Variables : There are two different categorical variables (Stroke patient vs control and whether the subject lives in the same household as a smoker). Living with a smoker (or not) is the natural explanatory variable and having a stroke (or not) is the natural response variable in this situation.
• Null Hypothesis : There is no relationship between whether or not a person has a stroke and whether or not a person lives with a smoker (odds ratio between stroke and second-hand smoke situation is = 1).
• Alternative Hypothesis : There is a relationship between whether or not a person has a stroke and whether or not a person lives with a smoker (odds ratio between stroke and second-hand smoke situation is > 1). This is a one-tailed alternative.

This research question might also be addressed like example 11.4 by making the hypotheses about comparing the proportion of stroke patients that live with smokers to the proportion of controls that live with smokers.

Example 10.7: Hypotheses about the relationship between Two Measurement Variables Section  

• Research Question : A financial analyst believes there might be a positive association between the change in a stock's price and the amount of the stock purchased by non-management employees the previous day (stock trading by management being under "insider-trading" regulatory restrictions).
• Variables : Daily price change information (the response variable) and previous day stock purchases by non-management employees (explanatory variable). These are two different measurement variables.
• Null Hypothesis : The correlation between the daily stock price change (\$) and the daily stock purchases by non-management employees (\$) = 0.
• Alternative Hypothesis : The correlation between the daily stock price change (\$) and the daily stock purchases by non-management employees (\$) > 0. This is a one-sided alternative hypothesis.

Example 10.8: Hypotheses about comparing the relationship between Two Measurement Variables in Two Samples Section  

• Research Question : Is there a linear relationship between the amount of the bill (\$) at a restaurant and the tip (\$) that was left. Is the strength of this association different for family restaurants than for fine dining restaurants?
• Variables : There are two different measurement variables. The size of the tip would depend on the size of the bill so the amount of the bill would be the explanatory variable and the size of the tip would be the response variable.
• Null Hypothesis : The correlation between the amount of the bill (\$) at a restaurant and the tip (\$) that was left is the same at family restaurants as it is at fine dining restaurants.
• Alternative Hypothesis : The correlation between the amount of the bill (\$) at a restaurant and the tip (\$) that was left is the difference at family restaurants then it is at fine dining restaurants. This is a two-sided alternative hypothesis.